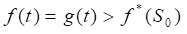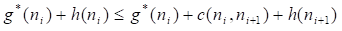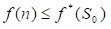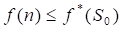人工智能搜索策略：A*算法

目录

在图搜索算法中，如果能在搜索的每一步都利用估价函数f(n)=g(n)+h(n)对Open表中的节点进行排序，则该搜索算法为A算法。由于估价函数中带有问题自身的启发性信息，因此，A算法又称为启发式搜索算法。
对启发式搜索算法，又可根据搜索过程中选择扩展节点的范围，将其分为全局择优搜索算法和局部择优搜索算法。

在全局择优搜索中，每当需要扩展节点时，总是从Open表的所有节点中选择一个估价函数值最小的节点进行扩展。其搜索过程可能描述如下：

（1）把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)；
（2）如果Open表为空，则问题无解，失败退出；
（3）把Open表的第一个节点取出放入Closed表，并记该节点为n；
（4）考察节点n是否为目标节点。若是，则找到了问题的解，成功退出；
（5）若节点n不可扩展，则转到第(2)步；
（6）扩展节点n，生成子节点ni(i=1,2,……)，计算每一个子节点的估价值f(ni) (i=1,2,……)，并为每一个子节点设置指向父节点的指针，然后将这些子节点放入Open表中；
（7）根据各节点的估价函数值，对Open表中的全部节点按从小到大的顺序重新进行排序；
（8）转第(2)步。

由于上述算法的第(7)步要对Open表中的全部节点按其估价函数值从小到大重新进行排序，这样在算法第(3)步取出的节点就一定是Open表的所有节点中估价函数值最小的一个节点。因此，它是一种全局择优的搜索方式。
对上述算法进一步分析还可以发现：如果取估价函数f(n)=g(n)，则它将退化为代价树的广度优先搜索；如果取估价函数f(n)=d(n)，则它将退化为广度优先搜索。可见，广度优先搜索和代价树的广度优先搜索是全局择优搜索的两个特例。

例 1： 八数码难题。 设问题的初始状态S0和目标状态Sg如图所示，估价函数与请用全局择优搜索解决该题。

解：这个问题的全局择优搜索树如图1所示。在图1中，每个节点旁边的数字是该节点的估价函数值。例如，对节点S2，其估价函数的计算为
f(S2)=d(S2)+W(S2)=2+2=4
从图1还可以看出，该问题的解为
S0 →S1 →S2 →S3 →Sg

图1 八数码难题的全局择优搜索树

在局部择优搜索中，每当需要扩展节点时，总是从刚生成的子节点中选择一个估价函数值最小的节点进行扩展。其搜索过程可描述如下：

(1)把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)；
(2)如果Open表为空，则问题无解，失败退出；
(3)把Open表的第一个节点取出放入Closed表，并记该节点为n；
(4)考察节点n是否为目标节点。若是，则找到了问题的解，成功退出；
(5)若节点n不可扩展，则转到第(2)步；
(6)扩展节点n，生成子节点ni(i=1,2,……)，计算每一个子节点的估价值f(ni) (i=1,2,……)，并按估价值从小到大的顺序依次放入Open表的首部，并为每一个子节点设置指向父节点的指针，然后转第(2)步。

由于这一算法的第六步仅仅是把刚生成的子节点按其估价函数值从小到大放入Open表中，这样在算法第(3)步取出的节点仅是刚生成的子节点中估价函数值最小的一个节点。因此，它是一种局部择优的搜索方式。
对这一算法进一步分析也可以发现：如果取估价函数f(n)=g(n)，则它将退化为代价树的深度优先搜索；如果取估价函数f(n)=d(n)，则它将退化为深度优先搜索。可见，深度优先搜索和代价树的深度优先搜索是局部择优搜索的两个特例。

上一节讨论的启发式搜索算法，都没有对估价函数f(n)做任何限制。实际上，估价函数对搜索过程是十分重要的，如果选择不当，则有可能找不到问题的解，或者找到的不是问题的最优解。为此，需要对估价函数进行某些限制。A*算法就是对估价函数加上一些限制后得到的一种启发式搜索算法。
假设f*(n)为从初始节点S0出发，约束经过节点n到达目标节点的最小代价值。估价函数f(n)则是f*(n)的估计值。
显然，f*(n)应由以下两部分所组成：

一部分是从初始节点S0到节点n的最小代价，记为g*(n)；

另一部分是从节点n到目标节点的最小代价，记为h*(n)，当问题有多个目标节点时，应选取其中代价最小的一个。

因此有 f*(n)=g*(n) +h*(n)
把估价函数f(n)与 f*(n)相比

g(n)是对g*(n)的一个估计

h(n)是对h*(n)的一个估计。

在这两个估计中，尽管g(n)的值容易计算，但它不一定就是从初始节点S0到节点n的真正最小代价，很有可能从初始节点S0到节点n的真正最小代价还没有找到，故有

一般来说，对任意一个状态空间图，当从初始节点到目标节点有路径存在时，如果搜索算法能在有限步内找到一条从初始节点到目标节点的最佳路径，并在此路径上结束，则称该搜索算法是可纳的。A*算法是可采纳的。下面我们分三步来证明这一结论。

定理1 对有限图，如果从初始节点S0到目标节点Sg有路径存在，则算法A*一定成功结束。
定理1 证明：
首先证明算法必定会结束。由于搜索图为有限图，如果算法能找到解，则会成功结束；如果算法找不到解，则必然会由于Open表变空而结束。因此，A*算法必然会结束。
然后证明算法一定会成功结束。由于至少存在一条由初始节点到目标节点的路径，设此路径
S0= n0，n1 ，…，nk =Sg
算法开始时，节点n0在Open表中，而且路径中任一节点ni离开Open表后，其后继节点ni+1必然进入Open表，这样，在Open表变为空之前，目标节点必然出现在Open表中。因此，算法必定会成功结束。

引理0 在最佳路径上的所有节点n的f值都应相等，即f(n)=f*(S0)

引理1 对无限图，如果从初始节点S0到目标节点Sg有路径存在，且A*算法不终止的话，则从Open表中选出的节点必将具有任意大的f值。
引理1 证明：
设d*(n)是A生成的从初始节点S0到节点n的最短路径长度，由于搜索图中每条边的代价都是一个正数，令这些正数中最小的一个数是e,则有

定理2 对无限图，若从初始节点S0到目标节点t有路径存在，则A*算法必然会结束。
证明：（反证法）假设A算法不结束，又引理5.1知Open表中的节点有任意大的f值，这与引理2的结论相矛盾，因此，A算法只能成功结束。

推论1 Open表中任一具有

定理3 A算法是可采纳的，即若存在从初始节点S0到目标节点Sg的路径，则A算法必能结束在最佳路径上。
证明：证明过程分以下两步进行：
先证明A*算法一定能够终止在某个目标节点上。
由定理1和定理2可知，无论是对有限图还是无限图，A算法都能够找到某个目标节点而结束。
**再证明A算法只能终止在最佳路径上（反证法）。**
假设A算法未能终止在最佳路径上，而是终止在某个目标节点t处，则有

在A*算法中，对任何被扩展的任一节点n，都有

A算法的搜索效率很大程度上取决于估价函数 h(n)。一般说来，在满足**h(n)≤h(n)**的前提下，h(n)的值越大越好。h(n)的值越大，说明它携带的启发性信息越多，A算法搜索时扩展的节点就越少，搜索的效率就越高?
A算法的这一特性也称为信息性。下面通过一个定理来描述这一特性。

定理4 设有两个A算法A1和A2*，它们有
A1*：f1(n)=g1(n)+h1(n)
A2*：f2(n)=g2(n)+h2(n)
如果A2比A1有更多的启发性信息，即对所有非目标节点均有
h2(n)> h1(n)
则在搜索过程中，被A2扩展的节点也必然被A1扩展，即A1扩展的节点不会比A2扩展的节点少，亦即A2扩展的节点集是A1扩展的节点集的子集。
证明：（用数学归纳法）
(1)对深度d(n)=0的节点，即n为初始节点S0，如果n为目标节点，则A1和A2都不扩展n；如果n不是目标节点，则A1和A2都要扩展n。
(2)假设对A2搜索树中d(n)=k的任意节点n，结论成立，即A1也扩展了这些节点。
(3)证明A2搜索树中d(n)=k+1的任意节点n，也要由A1扩展（用反证法）。
假设A2搜索树上有一个满足d(n)=k+1的节点n, A2扩展了该节点，但A1没有扩展它。根据第(2)条的假设，知道A1扩展了节点n的父节点。因此，n必定在A1的Open表中。既然节点n没有被A1扩展，则有
f1(n)≥f*(S0)
即 g1(n)+h1(n) ≥f*(S0)
但由于d=k时，A2扩展的节点A1也一定扩展，故有
g1(n)≤g2(n)
因此有 -g1(n) ≥ -g2(n)
因此有
h1(n)≥f*(S0)-g1(n) ≥f*(S0)-g2(n)
h1(n)≥f*(S0)-g2(n)
另一方面，由于A2扩展了n，因此有
f2(n) ≤f(S0)
即 g2(n)+h2(n) ≤f*(S0)
亦即 h2(n) ≤f*(S0)- g2(n)
f*(S0)- g2(n) ≥h2(n)
所以有 h1(n) ≥ h2(n)
这与我们最初假设的h1(n) < h2(n)矛盾，因此反证法的假设不成立。

在A*算法中，每当扩展一个节点n时，都需要检查其子节点是否已在Open表或Closed表中。对于那些已在Open表中的子节点，需要决定是否调整指向其父节点的指针；对于那些已在Closed表中的子节点，除了需要决定是否调整其指向父节点的指针外，还需要决定是否调整其子节点的后继节点的父指针。这就增加了搜索的代价。如果我们能够保证，每当扩展一个节点时就已经找到了通往这个节点的最佳路径，就没有必要再去检查其后继节点是否已在Closed表中，原因是Closed表中的节点都已经找到了通往该节点的最佳路径。为满足这一要求，我们需要=启发函数h(n)增加单调性限制。

定义1 如果启发函数满足以下两个条件：
h(Sg)=0；
对任意节点ni及其任意子节点nj,都有

定理5 如果h满足单调条件，则当A*算法扩展节点n时，该节点就找到了通往它的最佳路径，即

例 2 A*算法解决八数码难题

在例1中，我们取h（n）=W（n）。尽管我们对h*（n）不能确切知道，但采用单位代价时，通过对“不在位”数码个数的估计，可以得出至少要移动W（n）.因为，例1所定义的和h（n）满足A算法的限制条件。
这里再取另一种启发函数h(n)=P（n）， P（n）定义为每个数码与目标位置之间距离（不考虑夹在其间的数码）的总和，同样要判定至少要移动P（n）步才能达到目标，因此有 ，即满足A算法的限制条件。其搜索过程所得到的搜索树如图2所示。在该图中，节点旁边虽然没有标出P（n）的值p,但却标出了估计函数f（n）的f值。对解路径，还给出了各个结点的g* （n）和h*（n）的g值和h值。从这些值还可以看出，最佳路径上的节点都有 f*=g*+h*=4.
图2 A*算法解决八数码难题

例3 修道士和野人问题
用m表示左岸的修道士人数，c表示左岸的野人数，b表示左岸的船数，用三元组（m,c,b）表示问题的状态。

对A算法，首先需要确定评估函数。设g(n)=d(n),h(n)=m+c-2b,则有
f(n)=g(n)+h(n)=d(n)+m+c-2b
其中，d(n)为节点的深度。通过分析可知**h (n)<= h(n),满足A*算法的限制条件**。
M—C问题的搜索过程如图 3 所示。在该图中，每个节点旁边还标示了该节点的h值和f值。
图3 修道士和野人问题

A算法在搜索过程中open表和close表中实际上是存储一棵树，但这棵树的树干会经常变动，许多节点常会改变父子关系。见下图
原因是h(n)的单调性

• 最佳路径上的所有节点的f值都应相等
• g(n)是对g(n)的估计，且g(n)>0
• h(n)是对h(n)的下界，即对任意节点n均有*

• Open表中任一具有

设有两个A算法A1和A2*，它们有
A1*：f1(n)=g1(n)+h1(n)
A2*：f2(n)=g2(n)+h2(n)
如果A2比A1有更多的启发性信息，即对所有非目标节点均有
h2(n)> h1(n)
则在搜索过程中，被A2扩展的节点也必然被A1扩展，即A1扩展的节点不会比A2扩展的节点少，亦即A2扩展的节点集是A1扩展的节点集的子集。

• 如果启发函数满足以下两个条件：
• （1） h(Sg)=0；
• （2） 对任意节点ni及其任意子节点nj,都有